誤差や公差の複数積み重ねに対する二乗和導入の指導
公開日: 2023年6月5日 | 最終更新日: 2024年1月2日

誤差や公差の積み重ねというのは様々な研究開発や製造生産現場で生じる事象の一つです。
誤差に関するものとしては、例えば実験や試験において使用する複数原料を投入する際の重量バラツキ、製造生産現場では複数の設備機械の稼働時間や複数の部品から形成される金型温度といったものがあります。
公差の積み重ねとしては複数の部品から構成される製品を設計する際、
想定すべき組み立時の製品寸法のばらつき、
生産製造現場だと複数層に重ね塗りする際の塗膜の厚みばらつき等が例になります。
今回は上記の公差積み重ねである、
「複数の部品を組み合わせて一つの製品にするにあたり、その組み立てられた製品の寸法バラツキの考え方」
を一例に、実際に顧問先企業で技術者育成の観点で指導を行った事例を引き合いに出しながら、リーダーや管理職の方が取り組むべきことについて解説します。
最初は現場の技術者がどう考えるかを発言させる
その顧問先企業で行われていたのは、
ある3種類の部品を厚さ方向に組み立てて一つの製品にするというものに関し、
図面公差の妥当性を検証するという設計評価会でした。
私自身も顧問として同席していました。
その会において設計者である技術者が、
「最終製品は子部品a、b、cで構成されており、それぞれプロジェクターで示した図面による形状、並びに公差で試作を行いたい」
と発言しました。
見ると3枚の子部品図面中の二次元寸法に公差がそれぞれ振られていました。
試作図面では公差が抜けがちな企業に比べるときちんとしている印象を受けました。
議論になったのは、
・コストがどのくらいになるのか
・リードタイムはどのくらいになるのか
・二社購買にするのか
といった内容が多かったと記憶しています。
そのような中で当社側から出席していた私が問いかけたのは、
「a、b、cという3つの子部品を厚み方向に重ねて最終製品を組み立てるようですが、最終製品の厚み寸法のばらつきはどのくらいを想定していますか」
ということでした。
当然ながら最終製品の厚みがばらつくと、
この最終製品を他のシステムにインストールするときにはまらなかったり、
ガタツキが多くなったりする可能性を感じたためでした。
何より組み立てられた製品の品質管理をどうするかについても、
組み立て製品の状況を想定すべきというのも念頭にありました。
この問いかけに対する設計者である技術者の答えは、
「a、b、cの公差をすべて足したものを考えています」
とのことでした。
このようにまずは現場の技術者がどのように考えるのかを問いかけるということが、技術者育成では重要となります。
※関連コラム
二乗和という考え方があることを伝える
その意見を聞いた後に私が伝えたことは、
「その考えは間違っていません。しかし、公差の積み重ねが起こる最終製品として想定すべき公差としてかなり大きいと感じませんか。」
ということでした。
仮に公差の示す確率密度関数が釣り鐘形状の正規分布だったとすると、そのまま公差を足していく、例えば
「部品a、b、cの公差がそれぞれ±0.1mmの場合に±0.3mm」
とした場合、確率密度関数の両端付近の事象が3つの子部品で同時に生じるということになるからです。
ホワイトボードに3つの釣り鐘形状を書き、
それぞれの端だけが同時に起こる可能性が低いということを視覚的に示すことを心がけました。
これは言葉や文章だけではイメージが膨らみにくいということへの対応で、技術者が説明の際に図を書いて説明するという選択肢を持たせるという指導の観点も入っています。
そして公差の積み重ねということに対する考え方の一つとして、
「二乗和」
があることを伝えました。
例えば子部品a、b、cの厚み方向の公差がすべて±0.1mmの場合、二乗和をベースに公差を考えると
![]()
になります。よって、二乗和をベースに考えると、
±0.173mm程度の数値
がa、b、cという3つの製品を厚み方向に重ねて組み立てた場合に想定すべき公差となるのです。
すべての公差をそのまま加算した±0.3mmと比べると4割程度小さな値となっていることがわかります。
まずこの段階でそのまま加えるというという考えにこだわらず、
二乗和という考え方で公差の積み重ねを捉えるという観点を技術者に理解してもらいます。
二乗和の考え方を知らなかった技術者の多くは、
専門性至上主義の考えから興味を示すと思います。
新しい知識が習得できるという動機付けがあるためです。
このように日々の業務に関連したものに異なる技術的な考え方が存在することを伝えるのも、
技術者育成の観点ではマンネリ化を防ぐという意味でも重要になります。
伸びしろの有りそうな技術者にはその数学的な理論を調べさせる
もし教育対象である技術者の中に見込みがありそうな方がいる場合、当社からは
「今お伝えしたことに関する数学的な理論の概要を調べ、次回教えてください」
と伝えることがあります。今回も該当する技術者の方が複数いたため、同じような投げかけを行いました。
これは技術者の普遍的スキルの一つである
「グローバル技術言語力」
を構成する
「数字力、数学力」
に関する指導が目的にあります。
※関連コラム
第10回 技術者のグローバル化に必要な数学力と文章作成力の鍛え方 日刊工業新聞「機械設計」連載
以上の通り、
「先行して実務に使えるという意識を技術者に持たせた”後”で、その理論的な部分を能動的に調べさせることで能動的な活動を後押しする」
という流れが技術者育成では重要であることがお分かりになるかもしれません。
知識を実践力を伴う「知恵」まで昇華させる必要があるためです。
数学的な肉付けは考え方を最初に教えた上で数式をベースに指導する
課題を与えた技術者がどの程度の答えを用意できるかによりますが、
例えば私は以下のような答えを予め用意しておきました。
顧問先企業の技術者はそれなりに調べ、正規分布をベースに考えるまでは話をしてくれましたが、合致性の検定が抜けており、妥当性の検証についても感覚論で締めくくっていたため、以下のような解説は納得を後押しするものとなったと考えています。
プラスとマイナスの公差絶対値が同じ場合は正規分布が前提のため検定が必要
顧問先企業に関わらず多くの企業では正規分布を前提に議論を進めることがあります。
標準偏差という言葉を使うといったものがその一例です。
標準偏差は正規分布が成立する母集団で用いることができる考え方です。
例えば確率密度関数の検定の一つとしてAnderson Darling検定があります。
この検定は正規分布への合致性を評価することが可能です。
当社のもう一つの事業であるFRP関連の知見を応用することで、
データの確率密度関数モデル合致性を検定で調べる必要がある、
ということを伝えることは今回の事例に限らず多くあります。
※参照URL(当社のFRP技術指導事業の内容になります)
「 機械設計 」連載 第二十二回 取得したFRP 静的材料データは本当に正規分布として扱っていいのか
今回の例で言うと子部品を複数試作した段階で、各子部品の厚み計測結果の数値が正規分布を想定して問題ないか、ということを予め確認するよう提案しました。
公差の積み重ね評価に用いる二乗和は正規分布が前提だからです。
数学的な前提を、このように一つひとつ丁寧に押さえさせる重要性を技術者に理解させるのも技術者育成では重要です。
二乗和が公差の積み重ねに使えると考えるのに妥当な数学的根拠の概要をおさえる
詳細というよりもイメージを捉えながら二乗和を用いた考え方が、
公差の積み重ねの評価に妥当であることを理解させることが重要です。
実際に顧問先企業で話をした概要を以下に示します。
事例として用いたのが独立したxとyが、ランダムな誤差の影響を受けるとします。
上記を例にすると、子部品aとbが別々に製造され、そして厚みを計測されているとすれば、
これらは独立した関係にあるといった想定と同じになります。
例えば2つの子部品を想定した特定の値、例えば厚みの計測値をとる確率は、正規分布を前提とするとそれぞれ以下の式で示されます。
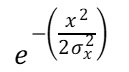 -(1)
-(1)
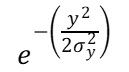 -(2)
-(2)
これらの式は正規分布の確率密度関数の変数部分、
すなわちネイピア数の部分を抽出しています。
ここで2つの部品の公差の積み重ねをイメージした[x+y]が特定の値を得る確率を計算する場合、(1)と(2)のそれぞれの式の積で求まるため、
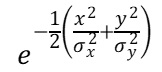
となります。それぞれ独立しているため掛け算で確率を計算できるのがポイントです。
このうち
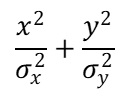
という部分の式をσx^2=A、σy^2=Bとして変形すると、以下のようになります。
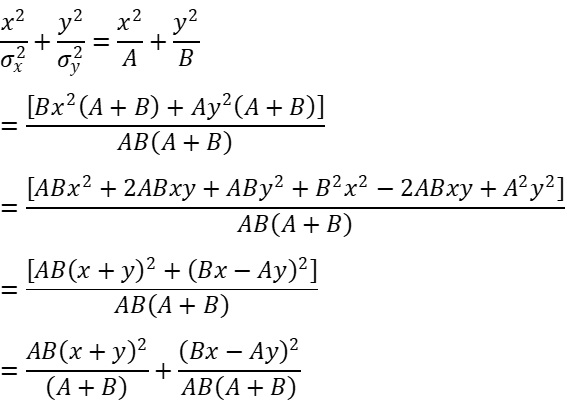
計算のロジックとしては、いかにして評価をしたい[x+y]を導き出すかです。
ここで第一項の[(x+y)^2/(A+B)]に着目すると、これが(x+y)というxとyの加算に関する正規分布の確率密度関数のネイピア数の乗数の変数部分になっており、その場合(A+B)、すなわち
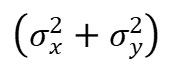
が”分散”になっていることがわかります。
つまり、分散の標準偏差が誤差を示していると考えれば、
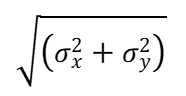
が互いに独立したxとyのばらつき(標準偏差に相当)するといえるのです。
厳密にはもう少し肉付けが必要ですが、上記のような式変形によって二乗和によるばらつきの評価が、正規分布を前提とした考え方により明確化されるということを技術者に理解させることができました。
上記の内容を理解するには正規分布の確率密度関数のイメージができていることが前提で、2つの独立した確率密度関数を掛け合わせることでその確率を算出し、その後の式変形で(x+y)という変数を正規分布に合うよう考えることで、二乗和を土台としたばらつきの評価が可能になるということは、詳細は別としても概要を理解することができるのではないでしょうか。
このような考え方はどのような技術業務でも横展開が可能であり、
日常的な業務の中でもケースとして多く存在すると考えられます。
その際に数学的な理論を考えながら仕事をするという上記のアプローチが、
技術者育成における最重要の普遍的スキルの醸成に不可欠です。
いかがでしたでしょうか。
今回は技術者育成の実例のうち、公差の積み重ねということを例としたものをご紹介しました。
一見手間がかかって大変かもしれませんが、技術者が技術的なスキルを高めるために必要な要素が多く含まれていることがわかるかと思います。
技術者育成というのは単発的な研修やセミナーに加え、
日常的な技術業務に即した丁寧な誘導が本質となります。
技術者を抱えるリーダーや管理職の方々に、
是非実践いただきたいやり方の一つです。
技術者育成に関するご相談や詳細情報をご希望の方は こちら
技術者育成の主な事業については、以下のリンクをご覧ください:






