グラフで囲まれた面積をExcelだけで求める方法がわからない
公開日: 2023年11月20日 | 最終更新日: 2023年11月23日
技術評価を行った結果を踏まえて得られたグラフについて、
その面積を算出するのが必要となることがあります。
このような場面においてリーダーや管理職が技術者の普遍的スキル向上を狙う場合、
どのような指示を与えるべきかについて考えます。
グラフデータの面積を求めることは技術業務でよくある
グラフの面積を求める業務は、
技術職である技術者の方であればどこかで触れる機会があると思います。
化学系であれば、熱分析技術の一つであるDSCを用いた熱硬化性樹脂の硬化度算出や、
光学分析であるFT-IRを用いた反応進行評価が一例です。
DSCは示差走査熱量計といいます。
熱硬化性、すなわち熱によって重合反応が進む有機化合物を評価対象とした場合、
相転移の一種であるガラス転移温度に加え、
分析中の加熱によって進行する重合反応に伴う発熱反応ピークを捉えられることから、
当該ピーク面積変動からどの程度硬化が進行したかという硬化度を算出することが可能です。
また、FT-IRであれば特定の官能基(原子1つまたは原子団のことで、主として反応性の観点から分けられる化学構造のこと)の透過度、もしくは吸光度のピーク面積の増加や減少から、反応進行に伴う構造変化を捉えることができます。
当該面積の増加率や減少率は、反応進行率に置き換えられることから、
反応の進行度合いを見極める一指標となります。
機械系であれば成形工程における荷重(または圧力)プロファイルと、
その荷重負荷時間をそれぞれ縦軸と横軸にプロットすれば、
荷重と荷重負荷時間で囲まれた領域の面積は”仕事”に該当するものになります。
成形される製品の品質が低下しない範囲でこの面積を最小化できれば、
荷重と荷重負荷時間の最適化につながり、
工程の効率化に向けた議論の足掛かりとなります。
上記は限られた例にすぎませんが、
分析や設備稼働によって得られたデータを分析することを目的に、
プロットデータで構成されるグラフで囲まれた面積を求めことは、
研究開発に限らず、品質保証や製造・生産といった幅広い部門の技術者にとって基本業務といえるでしょう。
グラフデータの面積を求めることは分析機器付属のソフトで対応するのが一般的になっている
最近は分析機器に付属している解析ソフトの機能向上もあって、
グラフで囲まれた面積を求めるのはワンクリックでできるようになりました。
言い換えるとソフトの使い方さえ身につければ、
多くの技術者にとって定常”作業”となります。
しかし若手技術者が何も考えずにソフト依存でしかグラフ面積を求められないという状態では、
例えばそのようなソフトが付属していない場合等、
自力で面積を求めることが求められる場面で何もできないことになります。
このようなリスクに加え、より柔軟に業務に対応できるようにする意味でも、
リーダーや管理職は技術者の普遍的スキル向上の観点を取り入れた業務指示を出すことが求められます。
技術者の普遍的スキルはあって当たり前の利便性が失われたときに力を発揮する
単純作業は自動化をはじめとした情報化技術等によって高速かつ高精度で行うことが可能な時代です。
これはこれで正解でしょう。
より生産的な技術業務を推進すべき技術者が、単純作業だけに従事するのはあまりにも勿体ないからです。
ただ、忘れてはいけないことがあります。
どのような技術業務に従事する技術者であっても、
その力量が試されるのは定常状態ではなく、
「不測の事態が生じて混乱している状態」
であることです。
上記の混乱状態下で、課題解決に導くことがすべての技術者に求められるのです。
このような行動を起こす際に必須となるのが、”技術者の普遍的スキル”です。
今回グラフの面積を求めるという技術業務を一例に、
どのようにしてこのスキルを向上させるきっかけにつなげればいいかを解説します。
グラフで囲まれた面積を算出するために必要な数学理論は何かを若手技術者に問いかける
リーダーや管理職から若手技術者に投げかけるべき最初の一言は何でしょうか。
それは、
「面積を簡単に算出できるソフトが仮に無い場合、どのような数学理論を使うべきだと考えるか」
という言葉です。
技術者の普遍的スキルは本質的な部分に関わるため、
常に土台となる理論を意識させることが肝要です。
今回でいえば、そもそもどのような考え方の理論を使って取り組むべきかという、
よりどころとなる理論を意識させることがポイントになります。
事例としてご紹介しているグラフで囲まれた面積の場合、用いるべき数学理論は
「積分法」
です。
今の教育課程でいうと主として高校数学IIIの範囲になります。
よって、高校で数学IIIを履修していない場合、
その技術者に向けた参考書(高校の教科書でもいいと思います)を用意する必要があるかもしれません。
インターネットの情報は玉石混交なので気を付けなければいけませんが、
最近はプロの講師等がわかりやすい動画を公開している場合もあるため、
そちらを学習の一助として使うことも選択肢の一つとなります。
※積分法を解説する動画の一例
https://www.youtube.com/playlist?list=PLDnhF1CbeSZlJ8DBtSXteotGV0RK9vXQZ
ただし、学校数学と違って与えられた問題を解くことが目的ではなく、
目の前に立ちはだかる”課題を解決する”のにどの知識が必要かを見極めるということが重要です。
例えば上記の動画でいえば、最優先で必要なのは定積分に関する動画#21になります。
尚、面積算出と積分の関係を知りたいということであれば#11も対象といえるかもしれません。
まず#21を見て、参考書を読み、欠けている知識を補完しながら、
グラフで囲まれた面積を求めるというのはどういうことかを理解させるよう、
若手技術者を誘導することがリーダーや管理職に求められます。
上記の取り組みは、技術者の普遍的スキルのうち
「グローバル技術言語力」
を鍛錬させる典型的な取り組みになります。
本スキルについては、過去のコラムや連載でも取り上げたことがあります。
※参照コラム、連載
第10回 技術者のグローバル化に必要な数学力と文章作成力の鍛え方 日刊工業新聞「機械設計」連載
機器に付属するソフト等を使わず、Excel等の一般的な表計算ソフトだけを使わせる
まず一度、機器に付属するソフトを用いてグラフで囲まれた面積を若手技術者に算出させます。
これが最終的な答えの一つになります(正確には範囲の指定方法によって数値が変動するため、答えの参照値という位置づけです)。
その上で機器に付属するソフト等を使わず、Excel等の一般的な表計算ソフトだけを使わせるということに取り組ませるのです。
このような手段が限られた中で技術業務を行う時、
技術者は本当の意味での力量を試されることになります。
シミュレーションとはいえ、若手技術者は不測の事態が生じて混乱している状態に置かれるからです。
期限を区切って取り組ませ、結果が出なければ一事例を教える
すらすらできてしまう若手技術者もいるかもしれませんが、
固まってしまう技術者もいると思います。
どちらにせよ、リーダーや管理職は期限を区切ることが重要です。
望ましい期限は2時間程度でしょうか。
技術者の普遍的スキルは、時間的緊張感のある場面でのみ向上します。
のんびりとやっていてはだめなのです。
有事に求められるのは瞬発力です。
2時間経過して、答えが出ずとも道筋が出せていれば問題ありません。
全く手つかずの場合は、ある程度リーダーや管理職も事例を示しながら一緒に考えることが重要です。
グラフの面積を求める具体例
ここで簡単な事例を示してみたいと思います。
今回模擬的に用意したのは
![]()
というグラフです。面積を求めたいxの範囲は以下の通りとします。
![]()
これは私が任意に作った関数ですが、
実際に分析結果チャートがある場合は、
それをCSVで吐き出してグラフ化し、近似線の関数を算出するといった対応が必要です。
このグラフはx=0.33付近で極小値を迎える曲線グラフになります。
実際のグラフは下図のようなイメージです。
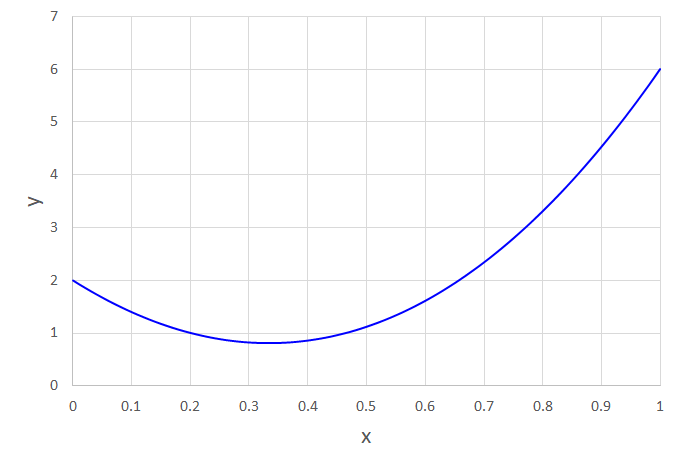
求めたい面積は関数グラフと0以上1以下のX軸と、
Xが0の時に関数グラフのY軸との交点と0点を結んだ線、
そしてXが1の時にY軸に平行な垂線を引いて囲まれた領域とします。
グラフで囲まれた面積を台形を積み重ねたものと読み替える
積分法の基本を理解すれば、面積をそのまま直接求めるのではなく、
X軸を短辺とする細長い四角形の足し算として置き換えることができます。
この置き換えの考え方を理解できるかが重要です。
数学的理論を意識しながら、視点を変えるというトレーニングになるからです。
異なるX値で刻みながら、囲まれる台形の面積を求める
近似はよりシンプルにするのであれば長方形ですが、
今回評価対象としているのは曲線ですので、
台形の方がより精度が高まると期待されます。
例えば0.1刻みと0.01刻みでXの数値を最大値である1まで表計算ソフトに入力し、
上記の関数の数値に代入した結果をYの値として当該ソフト、例えばExcelで計算させます。
ここで出てきたXとYの数値の組み合わせについて、
隣り合うデータ間についてXの数値の差異(Xn+1 – Xn)を台形の高さh、
その際の関数Yの数値(例:Yn+1、Yn)をそれぞれ上底と下底とすれば、
n番目のデータとn+1番目のデータで囲まれた面積(An+1)は下式で算出できます。
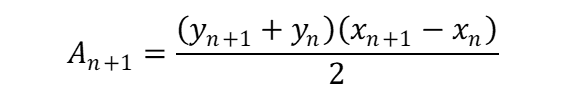
今回でいえばXが0から1の範囲、この計算を0.01刻みであれば100個、
0.1刻みであれば10個の台形の面積を算出し、
全て合算することでグラフで囲まれた面積を算出できます。
尚、実際にExcelで計算すると以下のようになります。
Xが0.01刻みの場合:2.083525
Xが0.1刻みの場合:2.1025
手計算で行う定積分の数値や解析ソフトで算出した値と比較する
ここで終わりにしないことが重要です。
実はこの計算で最も精度が高いのは高校数学の定積分です。
![]()
という関数例の右辺を積分すると、
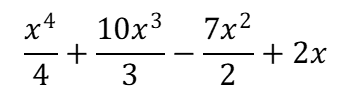
となります。
ここで前述した定積分の計算を0以上1以下の範囲で行うと、答えは2.083333333となります。
この数値は、関数を基本とした面積計算した際の答えとなります。
この結果と、例として0.1刻みと0.01刻みで算出された数値を比較すると、
0.01刻みで算出した面積2.083525が比較的近い数値となっていることがわかります。
つまり、X軸の数値を細かくすればするほどこの数値に近づくということが、
感覚論ではなく実際の数値として確認することができます。
このようにして数学的理論と技術者の実業務とのつながりを持たせることが、
技術者の普遍的スキル向上に大変有効です。
加えて例えば分析機器であれば付属している解析ソフトを用いて算出した面積と、
どの程度の誤差が生じるのかを比較することもできます。
このような一連の取り組みに関し、
算出方法の検討や結果の比較を技術報告書にまとめることで、
別の技術者の普遍的スキルである技術文章作成力も鍛えることが可能です。
小さな取り組みであっても、数学的理論を意識させる、理論をベースに実際に計算を実施する、得られた結果を比較の上、技術報告書としてまとめるという技術者の基本業務フローを体感することは、技術者の普遍的スキル向上に大変効果があります。
いかがでしたでしょうか。
技術者の普遍的スキルは重要なのは言うまでもありませんが、
その醸成は今回ご紹介したような大変地道なことの積み重ねになります。
技術者が普遍的スキルの一つであるグローバル技術言語力が実務に活用できることを、理論を含めて理解し、その有効性を実感することが当該スキル向上を土台とした技術者育成の本質です。
利便性だけを追い求めるのではなく、
その利便性を疑似的に失わせることで技術的な本質を見直すということが、
今の若手技術者には求められているのだと思います。
ご参考になれば幸いです。
技術者育成に関するご相談や詳細情報をご希望の方は こちら
技術者育成の主な事業については、以下のリンクをご覧ください:






